
Solid Rotation
Definite integrals could be used to calculate the area bounded between a and b. It could also find the volume of the area bounded between a and b if it were to rotate around the x-axes.
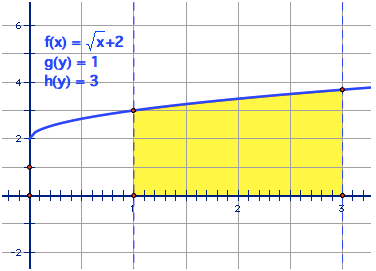
Imagine that the above area under the curve is rotating around the x-axis, creating a solid cone-like structure.
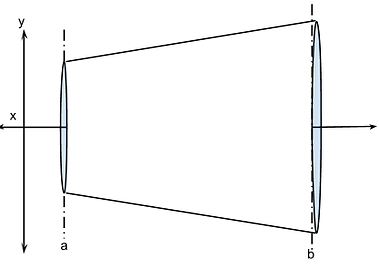
Just like we can approximate the area under the curve by breaking it down to trapezoids, left/right/midpoint rectangles, we would have to break this shape into thin disks. If we’re to find the exact volume of this solid, we would need to take the volumes of infinitely thin disks that is bounded by a and b. In order to do that, we need to take the integral. The height will be f(x). dx will represent the infinite amount of disks between a and b.
Since the disks are circular, the area of the circle formula is needed.
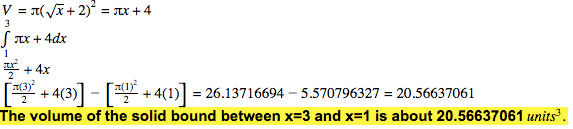
Plug in the function into the volume equation.
Solid Rotation Around Line Parallel to Coordinate Axis
But what if the area is not rotating around the axis, but around a line parallel to the axis?
Find the volume of the rotated area that is rotating around the line, f(y)=5 bounded by and y=4 between 1 and 2.
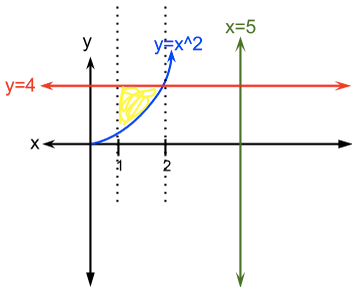
Imagine that the area is rotating around x=5.
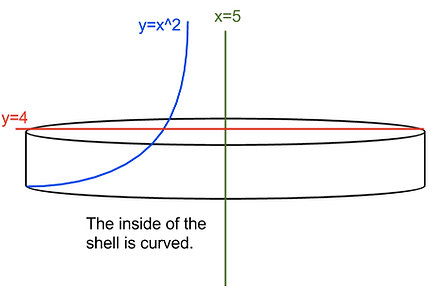
1.) Find the height of a rectangle inside the shell.
The width of a rectangle will always be dx.
The height of the rectangle will be the top function minus the bottom function since we’re dealing with an area bounded by two curves.
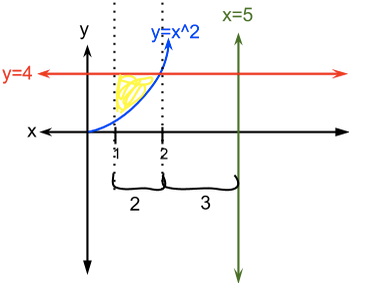
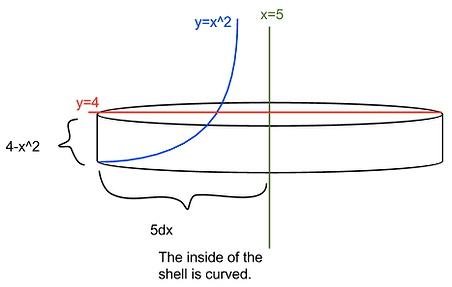
Since y=4 is at the top and is at the bottom, the height of the rectangle will be .
2.) Find the radius of the shell.
The radius will be the distance between y=5, the line that the area is rotated around, and the lower boundary.
3.) Find the circumference of the shell.

4.) Find the Surface Area of the shell.
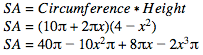
5.) Find the volume of the shell
-
Take the integral of the surface area if we want to sum up all the shells bounded between 2 and 1.
-
Multiply the surface area by the width of the shell, dx.
6.) Find the antiderivative.
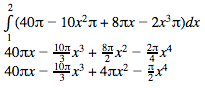
7.) Find F(2)-F(1).
