
Implicit Differentiation
Implicit Differentiation should be used when finding derivatives that involve both x and y. These equations are not functions. However, they have graphs and the function have slopes at all of its points, which means they are differentiable. It is mostly used when encountering problems that involves the Pythagorean Theorem.
-
Rewrite the expression with all y’s in parentheses.
-
Differentiate the expression in terms of x.
-
If the problem is asking for the slope or d/dy, solve for d/dy.
-
If the problem is asking for the equation of the tangent line, use the point and derivative to find y-intercept.
When we're finding the derivative of any expression that involves x's and y's, we need to keep in mind that y is not a function of x. So, it is helpful to put the letter y in parentheses as a reminder that y is a function of x, not a variable.
Sample Problem:
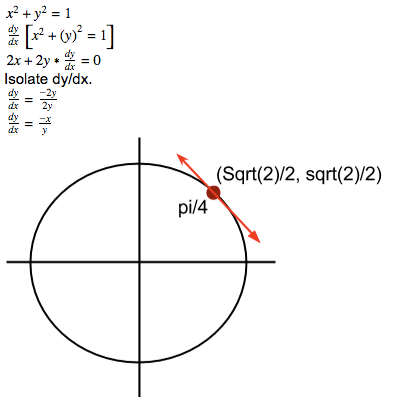
If we're to plug in the x and y values of any point on the circle, we could get the slope of the tangent line that intersects that point. In this case, if we were to plug in (sqrt(2)/2, sqrt(2)/2) into the equation, -1/y. The slope of the tangent line at pi/4 will be -1.

