
Derivative Rules

Find the derivative, .
*Notice how the derivatives are always a power less than the original terms.

General Exponential Rule:
In a fantastical village, Dragonaria, the population was 2,567 people in 1990. In 2015, the population risen up to 3,240. When will the population in Dragon in year 2020 and what is its rate of change?
Find the exponential equation that could model Dragonaria’s population.
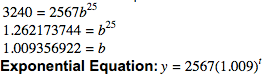
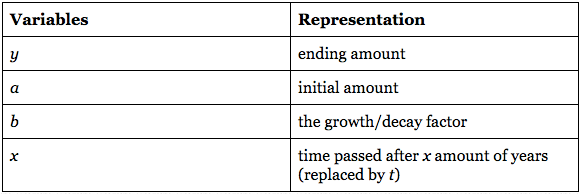
Since “a” represents the initial amount, 2,567 will be “a.” Plug in the “x” and “y” of the second ordered pair into their corresponding variables in order to find “b.”
Plug in 30 to “t” to find the population in year 2020 because 2020 is 30 years after 1990.

Find the derivative of the exponential equation.
Plug in 30 for “t” to find the rate of change in year 2020.

Trignometric Rules


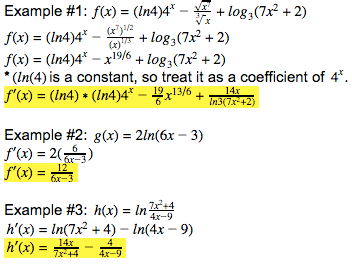
Find the derivative of the function, .
Use the Chain Rule, by multiplying the derivative of the outside and inside function together.
Drop the constant.
9.1---0
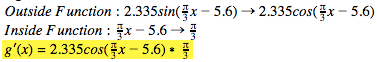

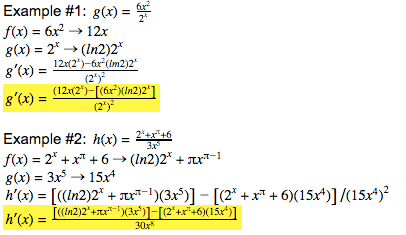

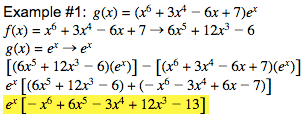

Example #2: The quantity,q, of roller skates sold depends on its selling price, p, in dollars. Thus, q=f(p). If f(200)=32,900 and f’(200)=-150, what is the total revenue, R, earned by the sales of roller skates when the p is 200?
Given: R=pq.
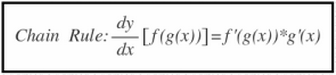
The chain rule is used to differentiate composite functions, f(g(x)). The chain rule statesthat the derivative of a composite function is equal to the product of the derivatives of the outside and inside functions, with the derivative of the outside function evaulated at the inside function.
This is an optimization problem that uses the product rule. For more optimization problems go to the optimization tab.
To solve this problem, we need an equation that will model the problem. Since we're finding the revenue, R=price*quantity is needed. Then, differentiate the revenue equation to incorporate f'(p) and p' into the diffentiated equation. Next, plug in the known values and solve for R.
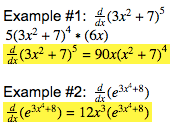
Example #3: Evan, a college freshman, plans to save money for his fourth year at Penn State University when his parents will no longer support him. So, he decides to put $3,000 in Conestoga Bank. He was told by the banker that he will earn 0.25% interest each year ("Savings Account Interest," Conestoga Bank). Write an equation to model how his bank account will be changing as a function of “t”, representing time in years. After you have found the equation, find how much he will have in his account after 4 years. Then, find the rate at which his bank account is growing after 4 years. Round final answers to the hundredths place.
In order to find the amount of money Evan have in his bank account after 4 year, we need to use the continuous interest formula.
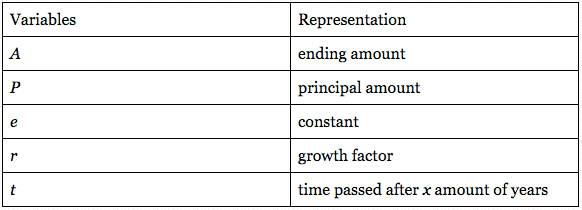
Step 1: We have all of the necessary components to find an equation.
A=unknown
P=$3,000
e=constant
r=0.25% (0.0025)
Equation
Step 2: Using the equation above, we can find how much money Evan will have in his savings account after 4 years by plugging 4 into “t”.

Step 3: In order to find the rate at which his bank account is growing, we need to find the derivative of the function by using the chain rule. The outside function will be 3,000e^0.0025t and the inside function would be 0.0025t. Since, e is considered a constant, not a variable, we could simply multiply 3,000 and e together to make one constant value.
