top of page

What is a Derivative?

Derivatives are all about slopes. The average rate of change is also incorporated as a part of derivatives. The following function is the average R.O.C formula for finding the slope between two points. 

where, f(a) and f(b) represent the y values and a and b represent the x values of their respective y values. 

Instantaneous rate of change is the slope of one specific point or the rate of change at that instant. It is also the number that the average velocity approaches as the intervals decrease. Graphically, the instantaneous R.O.C. is the slope of the tangent line that only intersects at that specific point. On the other hand, the average R.O.C. is the slope of the secant line between two points.  

 

We could use the average rate of change formula to find the instantaneous rate of change by using the numeric method, where we get to approximate the instantaneous rate of change by finding the Avg. R.O.C. between the point (desired x value and a point that is close to the x value.) 

 

Instantaneous R.O.C General Formula

Instantaneous Rate of Change

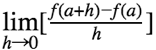
Determine the instantaneous rate of change of the

function,                                 at x=1 and x=-1.

 

  1. Graph the function

  2. Use a straightedge to draw a tangent line that intersects the point of interest. 

  3. Use the slope triangle to find the slope of the tangent line.  

 

The instantaneous rate of change at x=-1 is 10.88. The instantaneous rate of change at x=1 is 18.72. 

Find the instantaneous rate of change at                        at x=2. 

f’(2)=4

Average Rate of Change from x=1 to x=2. 

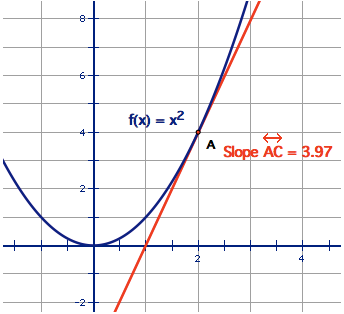
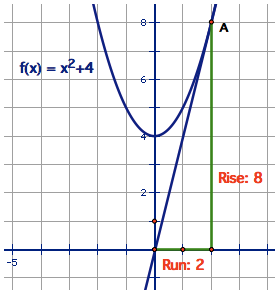
Instantaneous Rate of Change at x=2. 

Calculate Instantaneous R.O.C. Graphically

Calculate Instantaneous R.O.C. Algebrically

Plug in the a value into the instantaneous velocity formula.

 

 

 

Simplify the numerator 

*Notice how the constants cancelled out. This should happen every time with the other functions. 

 

 

 

 

 

 

 

 

 

 

Factor out a h from the denominator. 

 

 

 

*Remember the goal is to eliminate the h in the denominator so the limit will not be undefined. 

 

Plug in 0 for h. 

 

 

f’(1)=4

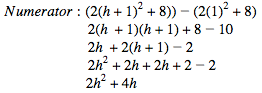
The derivative of f(x) could be denoted as f'(a). 

"f prime of a."

If the limit exist, then f(x) is differentiable at point a.

Differentiability
Graphically

Calculate Instantaneous R.O.C. Numerically

Derivatives are the rates of change or the velocities of specific sets of graphical data. It could be represented as a secant line between two points, slope between two points or it could be represented by a tangent line at one point, slope at a point. Finding and understanding derivatives are essential to find the rates at which trends are decreasing or increasing. 

 

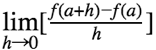
  • a represents the interval of interest

  • h variable represents the distance between the x value that you are trying to find and a point that is very close to the target x value. So, we could have a better estimate of the slope of the tangent line. Therefore, finding the instantaneous rate of change. 

 

Find the instantaneous rate of change for the function,                        , at x=1. 

 

 

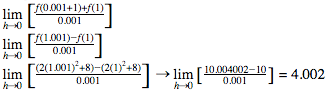
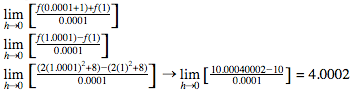
  1. To get a good estimate of the instantaneous velocity, we need to use 2-3 h values. (Use 0.001 and 0.0001 as h values) 

  2. Plug known values in the instantaneous velocity formula.

    • Plug in 1.001 and 1 into the function.

 

 

 

 

 

 

    • Plug in 1.0001 and 1 into the function.  

 

The In. R.O.C will be 4 because as the h value gets smaller it gets closer to 4. The answer could also be expressed as f’(1)=4. 

bottom of page